Next: Installer le code Up: Spectral gas properties Previous: Modèle FS-SNBCK Contents
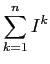 |
(1.29) | ||
| (1.30) |
Les paramètres du modèle de gaz gris qui sont le nombre de gaz gris ![]() , les coefficinets d'absorption
, les coefficinets d'absorption ![]() et les pondérations
et les pondérations ![]() ont été calculés par de nombreux auteurs pour la vapeur d'eau seule, pour des mélanges
ont été calculés par de nombreux auteurs pour la vapeur d'eau seule, pour des mélanges ![]() , ou mêm en prenant en compte le rayonnement de la suie. dans le cas de mélanges
, ou mêm en prenant en compte le rayonnement de la suie. dans le cas de mélanges ![]() , la tabulation doit être faire pour des valeurs données du rapport entre la pression partielle d'eau (
, la tabulation doit être faire pour des valeurs données du rapport entre la pression partielle d'eau (![]() ) et celle de
) et celle de ![]() (
(![]() ). Ces rapport de pressions
). Ces rapport de pressions
![]() sont couramment choisis égaux à 2, 1, ou 0.5. Le modèle choisi pour PRISSMA est un modèle à 3 gaz gris plus un gaz transparent, dont les paramètres ont été calculés pour des mélange
sont couramment choisis égaux à 2, 1, ou 0.5. Le modèle choisi pour PRISSMA est un modèle à 3 gaz gris plus un gaz transparent, dont les paramètres ont été calculés pour des mélange ![]() à pression atmosphérique et avec un rapport
à pression atmosphérique et avec un rapport
![]() correspondant par exemple à une situation de combustion méthane-air [#!Sou94!#]. Ces paramètres ont été calculés à partir de données spectrales SNB couvrant une région allant de
correspondant par exemple à une situation de combustion méthane-air [#!Sou94!#]. Ces paramètres ont été calculés à partir de données spectrales SNB couvrant une région allant de
![]() à
à
![]() . Elles ne couvrent donc pas la totalites du spectre utilisé dans le modèle SNB-CK, en particulier pour les grands nombres d'onde, mais prennent en compte les bandes les plus importantes pour
. Elles ne couvrent donc pas la totalites du spectre utilisé dans le modèle SNB-CK, en particulier pour les grands nombres d'onde, mais prennent en compte les bandes les plus importantes pour ![]() et
et ![]() .
.
Le modèle choisi comprenant 3 gaz gris, l'équation ![]() se reécrit:
se reécrit:
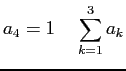 |
(1.32) |
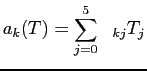 |
(1.33) |
Damien Poitou 2010-06-10