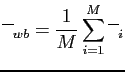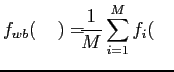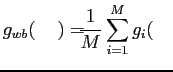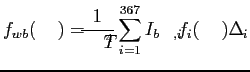En partant du modèle SNB-CK, Liu et al. [#!Liu99!#] proposent d'opérer des regroupements de bandes étroites voisines et d'effectuer ensuite les calculs sur ces bandes élargies. Alors, pour un regroupement de 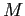 bandes étroites de même largeur, la transmittivité moyenne est donnée par:
bandes étroites de même largeur, la transmittivité moyenne est donnée par:
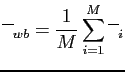 |
(1.23) |
où
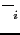 est la transmittivité moyenne de la ième bande étroite dans le regroupement des M bandes. La transmittivité moyenne sur la bande large est alors simplement la moyenne des transmittivités moyennes des bandes étroites qui la composent.
Si on considère maintenant une formulation en coefficients d'absorption, la fonction de distribution de la bande large est donnée par:
est la transmittivité moyenne de la ième bande étroite dans le regroupement des M bandes. La transmittivité moyenne sur la bande large est alors simplement la moyenne des transmittivités moyennes des bandes étroites qui la composent.
Si on considère maintenant une formulation en coefficients d'absorption, la fonction de distribution de la bande large est donnée par:
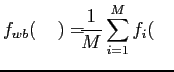 |
(1.24) |
où
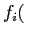 est la fonction de distribution des coefficients d'absorption dans la ième bande étroite. La fonction cumulée peut être obtenue de la même façon par:
est la fonction de distribution des coefficients d'absorption dans la ième bande étroite. La fonction cumulée peut être obtenue de la même façon par:
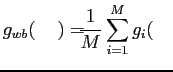 |
(1.25) |
Ce principe du regroupement de bandes introduit des erreurs dans l'hypothèse de bande étroite. En effet, plus on ajoute de bandes étroits voisines, et moins on peut considérer que la luminance du corps noir dans la bande est constante. Liu et al. [#!Liu99!#] soulignent cette source d'erreurs et recommandent de se limiter dans le nombre de bandes regroupées. Cependant, il est possible de tenir compte de la variation de la luminance du corps noir dans le différentes bandes regroupées par une pondération sur chaque bande étroite [#!Liu04a!#]. Il est alors possible de regrouper toutes les bandes pour obtenir le modèle FSCK. Dans ce modèle, toutes les bandes étroites sont regroupés et les fonctions 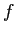 et
et 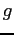 obtenues de ce regroupement à une température donnée sont exprimées par:
obtenues de ce regroupement à une température donnée sont exprimées par:
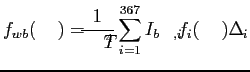 |
(1.26) |
où  est la constante de Stefan-Boltzmann,
est la constante de Stefan-Boltzmann,
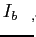 est la luminance du corps noir pour la bande étroite
est la luminance du corps noir pour la bande étroite 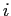 à la fréquence
à la fréquence  . La même pondération est affectée à la fonction cumulée:
. La même pondération est affectée à la fonction cumulée:
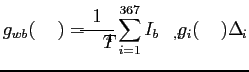 |
(1.27) |
L'utilisation pratique de ce modèle se fait en plusieurs étapes nécessitant l'inversion de la fonction g. En effet, pour réaliser l'intégrale de l'équation ![[*]](icons/crossref.png) , il faut connaître la valeur de la fonction
, il faut connaître la valeur de la fonction 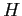 pour le coefficient d'absorption
pour le coefficient d'absorption  correspondant au point de quadrature
correspondant au point de quadrature 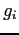 . On dispose au départ de la quadrature qui donne les valeurs de
. On dispose au départ de la quadrature qui donne les valeurs de 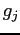 et les poids
et les poids 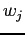 associés pour le spectre regroupé. Il faut alors chercher pour chaque valeur de
associés pour le spectre regroupé. Il faut alors chercher pour chaque valeur de 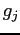 la valeur
la valeur 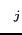 telle que l'équation
telle que l'équation ![[*]](icons/crossref.png) soit respectée. Pour une valeur de
soit respectée. Pour une valeur de 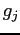 , cette opération se fait par dichotomie. Pour chaque valeur de
, cette opération se fait par dichotomie. Pour chaque valeur de  testée, on calcule donc la valeur de
testée, on calcule donc la valeur de 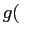 pour chaque bande, puis on calcule la valeur de
pour chaque bande, puis on calcule la valeur de 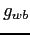 en utilisant l'équation
en utilisant l'équation ![[*]](icons/crossref.png) . La valeur maximale de départ prise pour
. La valeur maximale de départ prise pour 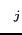 est de 10 fois la valeur maximale du paramètre
est de 10 fois la valeur maximale du paramètre
 pour l'ensemble des bandes étroites. Un critère d'arrêt de la dichotomie à 50 itérations a été introduit afin d'éviter des phénomènes de boucle infinie.
pour l'ensemble des bandes étroites. Un critère d'arrêt de la dichotomie à 50 itérations a été introduit afin d'éviter des phénomènes de boucle infinie.
L'inversion par dichotomie peut être consommatrice en temps de calcul et il sera donc souhaitable de rechercher une tabulation pour éviter cette opération . Toutefois, une fois cette opération effectuée, l'intégration spectrale se fait alors très rapidement, puisqu'il n'y a plus que 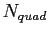 calculs spectraux à effectuer.
calculs spectraux à effectuer.
Damien Poitou
2010-06-10