Next: Modèle FS-SNBCK Up: Spectral gas properties Previous: Spectral gas properties Contents
![$\displaystyle \overline{\tau}_{\Delta \nu}(l)=exp \left[-\frac{\phi}{\pi} \left( \left( 1+ \frac{2 \pi \overline{\kappa} l}{\phi} \right)^{1/2} -1\right) \right]$](img76.png) |
(1.14) |
La fonction de distribution des coefficients d'absorptions pour le modèle de Malkmus a une expression analytique [#!Duf99!#] et est obtenue par :
On utilise alors l'expression de la fonction cumulée de la distribution des coefficients d'absorption comme variable de description spectrale (
![]() ), qui a comme expression analytique pour un modèle de Malkmus :
), qui a comme expression analytique pour un modèle de Malkmus :
Par cette opération, l'intégrale précédente (Eq. ![]() ) se réécrit:
) se réécrit:
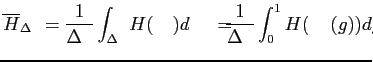 |
(1.18) |
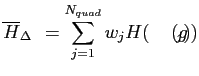 |
(1.19) |
A ce stade, pour traiter des milieux non homogènes et non isothermes, on fait une hypothèse supplémentaire afin de prendre en compte la déformation du spectre le long d'un chemin optique. Cette hypothèse consiste à considérer que toutes les raies d'une bande étroite se déforment de la même manière en fonction de la température. Autrement dit, on peut considérer que la quantité
![]() est constante quel que soit la fréquence dans la bande étroite. Cela revient également à considérer que la fonction
est constante quel que soit la fréquence dans la bande étroite. Cela revient également à considérer que la fonction ![]() est constante le long d'un chemin optique. C'est l'hypothèse des K corrélés ou hypothèse CK.
est constante le long d'un chemin optique. C'est l'hypothèse des K corrélés ou hypothèse CK.
Par ailleurs, le traitement du mélange de gaz est obtenu par le même modèle en suivant la méthode de Liu [#!Liu01!#] basée sur la limite optiquement mince et qui donne les paramètres d'un mélange de gaz en fonction des paramètres de ses constituants:
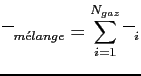 |
(1.20) |
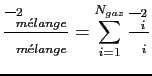 |
(1.21) |
Lors d'un calcul de terme source, les calculs radiatifs sont effectués
![]() fois de manière indépendantes, où
fois de manière indépendantes, où
![]() est le nombre de bandes étroites, de largeur
est le nombre de bandes étroites, de largeur
![]() considérées. Ces bandes permettent de considérer une région du spectre infrarouge allant de
considérées. Ces bandes permettent de considérer une région du spectre infrarouge allant de
![]() à
à
![]() .
.
![]() représente le nombre de points de quadratures pour chaque bande étroite. L'équation du terme source radiatif calculé est donnée par :
représente le nombre de points de quadratures pour chaque bande étroite. L'équation du terme source radiatif calculé est donnée par :
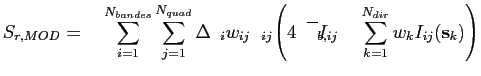 |
(1.22) |
Le modèle SNB-CK étant le modèle de propriétés radiatives des gaz disponible le plus précis dans PRISSMA, les résultats produits avec ce modèle serviront de résultats de référence pour les modèles FSCK et WSGG. Le code PRISSMA utilisé avec le modèle SNB-CK a fait l'objet de benchmarks avec d'autres codes et l'on pourra trouver des points de comparaison dans [#!Stanford!#].
Damien Poitou 2010-06-10