A simulation software often computes a configuration in a step response fashion. Indeed, it starts from an approximate initial state and iteratively advances towards a statistically converged state that satisfies the physical constraints of the model. In Computational Fluid Dynamics (CFD), for instance, the conservation laws are progressively enforced, resulting in global signals with similar characteristics. Consequently, before reaching a statistically steady state, there is a warm-up period unsatisfactory from the modeling point of view, that should be discarded in our data collection.
Traditionally, this warm-up is determined using a rule of thumb, which can be prone to errors. To address this issue, we present in this post a Python implementation of a method that can automatically estimate the appropriate amount of data to be discarded. This method is outlined in the research paper titled “Detection of initial transient and estimation of statistical error in time-resolved turbulent flow data” by Charles Mockett et al. (2010). You can find the paper at the following link: Mockett et al., 2010.
To illustrate these concepts of warm-up and statistically converged state, we takes the minimal temperature as a function of the time in a combustion chamber:
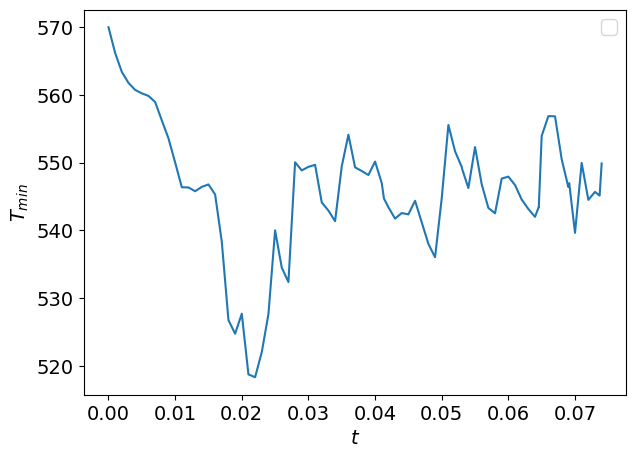
As you can see, the minimal temperature as a function of the time behaves differently before \(t \approx 0.03\) and after. Indeed, until \(t \approx 0.03\), the flow is evoloving from the initial conditions until the statistically steady state.
For reliable statistics and quantifications on the minimal temperature, we would like to get rid of the warm-up period and find the transient time \(t_t\) at which the system switches from the warm-up state towards the statistically steady state.
Mean and standard deviation of the signal
Before to dive in finding the transient time of the signal presented, some mathematical background is needed to explain the methodology.
Let’s imagine a time-dependent signal \(f(t)\) where \(t\) is the time. This signal is assumed to be extracted from a continuous stationary ergordic random processes. We can then define the mean \(\mu_f\) and the standard deviation \(\sigma_f\) of the signal as
where \(\mathbb{E}[X]\) is the expected value of \(X\). \(\mu_f\) and \(\sigma_f\) can only be obtained from infinite sample lengths. For a signal of length \(T = t_{end} - t_{ini}\) where \(t_{ini}\) and \(t_{end}\) are respectively the beginning and end of the signal, \(\mu_f\) and \(\sigma_f\) can be approximated by
For a finite number of samples \([f(t_0), f(t_1), \dots, f(t_n)]\) with \(t_0 < t_1 < \dots < t_n\) and \(t_n - t_0 = T\), this becomes
If now, we divide the signal \(f(t)\) into time-windows of length \(T_w\), the absolute statistical error on the estimate \(\hat{\phi}_{T_w}\) (\(= \hat{\mu}_{T_w}\) or \(\hat{\sigma}_{T_w}\)) for the time-windows length \(T_w\) compared to the estimate \(\hat{\phi}_{T}\) (respectively \(\hat{\mu}_{T}\) or \(\hat{\sigma}_{T}\)) for the full length of the signal \(T\) is given by
where \(<>\) denotes the average over all the time-windows. With this equation, the error as a function of the sample length can be estimated. Note that the accuracy of this error decreases as \(T_w\) becomes close to \(T\) since less windows are available to compute the error.
For the case of the bandwidth-limited Gaussian white noise, the error on the estimates \(\hat{\mu}_{T}\) and \(\hat{\sigma}_{T}\) as a function of the sample length \(T\) can directly be obtained through:
where \(B\) is the bandwidth. These approximations are valid for \(BT \geq 5\). Since \(\sigma_f\) is not known, this term is replaced by the best standard deviation estimate that is here \(\hat{\sigma}_T\). Also, to further detect the transient times, the authors of the article decided to use two bandwith parameters \(B_\mu\) and \(B_\sigma\). Thus, the errors on the estimates become:
The parameters \(B_\mu\) and \(B_\sigma\) are obtained as the lowest bandwidth values such as the curves of \(\epsilon[\hat{\phi}_T](T)\) intersect the ones of \(\epsilon[\hat{\phi}_{T_w}](T_w)\).
Here is the Python program to plot the errors estimated with the windows and with the bandwidth-limited Gaussian white noise:
import numpy as np
import scipy
from matplotlib import pyplot as plt
def eps_mean_windows(window_size: float, t: np.ndarray, samples: np.ndarray) -> float:
"""Computes the average error on the mean with all the time-windows
of length window_size of the signal.
"""
mean = samples.mean()
n_windows = int((t[-1] - t[0]) / window_size)
t_end = t[0] + n_windows * window_size
tw = np.linspace(t[0], t_end, n_windows + 1)
diff = [(samples[(tw[i] <= t) & (t < tw[i + 1])].mean() - mean) ** 2 for i in range(len(tw) - 1)]
return np.sqrt(np.mean(diff))
def eps_std_windows(window_size: float, t: np.ndarray, samples: np.ndarray) -> float:
"""Computes the average error on the standard deviation with all the time-windows
of length window_size of the signal.
"""
std = samples.std()
n_windows = int((t[-1] - t[0]) / window_size)
t_end = t[0] + n_windows * window_size
tw = np.linspace(t[0], t_end, n_windows + 1)
diff = [(samples[(tw[i] <= t) & (t < tw[i + 1])].std() - std) ** 2 for i in range(len(tw) - 1)]
return np.sqrt(np.mean(diff))
def compute_B_mean(window_size: float, t: np.ndarray, samples: np.ndarray) -> float:
"""Computes the B_mean parameter such that the errors on the mean given
by the time-windows and the Gaussian-White noise formulas are the same for the
window size considered. This function is needed to further fit the B_mean parameter.
"""
std = samples.std()
eps = eps_mean_windows(window_size, t, samples)
return 1 / (2 * window_size * eps**2) * std**2
def B_mean_fitting(t: np.ndarray, samples: np.ndarray) -> float:
"""Finds the lowest B_mean parameter such that the curve of the error
on the mean with the Gaussian white noise formula intersects the curve of the
error on the mean given with the time windows.
"""
# Bounds for the optimization. We choose the lower bound such that there are some samples
# in the window size and not too small for long range signals.
time_step = np.max(np.diff(t))
lb = max(10 * time_step, (t[-1] - t[0]) / 1000)
ub = (t[-1] - t[0]) / 2
bounds = ((lb, ub),)
# We consider ten starting points for the optimization.
window_size_ini = np.linspace(lb, ub, 10)
# We choose the Nelder-Mead method since gradient-based method is inefficient
# due to the noisy curve of the error with the time-windows.
B_mean = [optimize.minimize(compute_B_mean, window_size_ini[i], args=(t, samples), bounds=bounds, method="Nelder-Mead").fun for i in range(10)]
return np.min(B_mean)
def compute_B_std(window_size: float, t: np.ndarray, samples: np.ndarray) -> float:
"""Computes the B_std parameter such that the errors on the standard deviation given
by the time-windows and the Gaussian-White noise formulas are the same for the
window size considered. This function is needed to further fit the B_std parameter.
"""
std = samples.std()
eps = eps_std_windows(window_size, t, samples)
return 1 / (4 * window_size * eps**2) * std**2
def B_std_fitting(t: np.ndarray, samples: np.ndarray) -> float:
"""Finds the lowest B_std parameter such that the curve of the error
on the standard deviation with the Gaussian white noise formula intersects the curve of the
error on the standard deviation given with the time windows.
"""
time_step = np.max(np.diff(t))
lb = max(10 * time_step, (t[-1] - t[0]) / 1000)
ub = (t[-1] - t[0]) / 2
bounds = ((lb, ub),)
window_size_ini = np.linspace(lb, ub, 10)
B_std = [optimize.minimize(compute_B_std, window_size_ini[i], args=(t, samples), bounds=bounds, method="Nelder-Mead").fun for i in range(10)]
return np.min(B_std)
If we go back to the minimal temperature signal presented earlier, by running the following program, we ask this:
data = pd.read_csv('avbp_mmm.csv', sep=',')
t = data['atime'].to_numpy()
samples = data['T_min'].to_numpy()
std = samples.std()
B_mean = B_mean_fitting(t=t, samples=samples)
B_std = B_std_fitting(t=t, samples=samples)
windows_test = np.linspace(np.log(0.0005), np.log(0.99), 100)
windows_test = np.exp(windows_test)
eps_tw_mu_total = [eps_mean_windows(window_size, t, samples) for window_size in windows_test]
eps_tw_sigma_total = [eps_std_windows(window_size, t, samples) for window_size in windows_test]
We obtain the following figure:
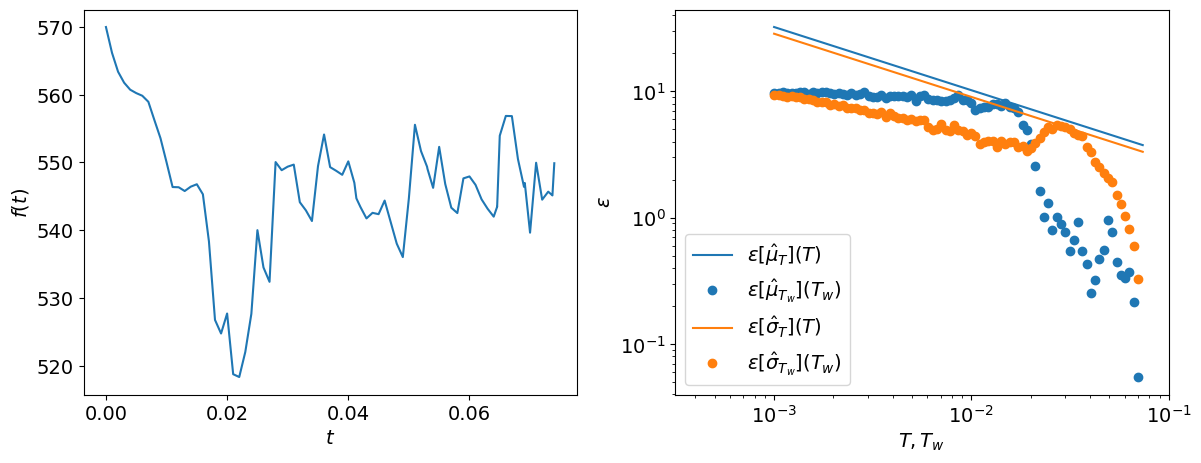
On the left, you can observe the original signal and on the right, the errors on the estimates of the mean and standard deviation with the bandwidth-limited Gaussian white noise formulas and windows estimates. Note that the error predicted with the bandwidth-limited Gaussian white noise are over-estimated compared to the error computed with the time-windows method. Still, since it is often preferable to over-estimate the error than to under-estimate it, this failure will not have a significant impact on the methodology.
Method to detect the transient times
To detect the transient times, the data obtained will successively be shortened starting from a time \(t \geq t_0\) to obtain a signal of length \(T^\prime = t_n - t\). If we call \(t_t\) the time at which occurs the end of the warm-up period, and \(T_t = t_n - t_t\) the length of the signal in the statistically steady state, the following hypothesis are considered:
-
for \(t < t_t\), the total error \(\epsilon[\hat{\mu}_{T^\prime}] \times \epsilon[\hat{\sigma}_{T^\prime}]\) (computed with the bandwidth-limited Gaussian noise formulas) is higher than \(\epsilon[\hat{\mu}_{T_t}] \times \epsilon[\hat{\sigma}_{T_t}]\). Indeed, the inclusion of the transient period in the computation of the mean and standard deviation is supposed to result in a distortion in at least one of these quantities and increase the errors on these predictions.
-
for \(t > t_t\), as we increase \(t\), the total error \(\epsilon[\hat{\mu}_{T^\prime}] \times \epsilon[\hat{\sigma}_{T^\prime}]\) begins to rise again since the error is inversely proportional to the time period considered.
For these reasons, the transient time is determined by finding \(T^\prime\), such that the total error \(\epsilon[\hat{\mu}_{T^\prime}] \times \epsilon[\hat{\sigma}_{T^\prime}]\) is minimized. As \(T^\prime\) becomes closer to \(T\), the statistical estimates become more inacurrate as less samples are provided and results in various local optima in the total error. For this reason, as in the original implementation, we set the limit \(T^\prime < T/2\). The following program will be used to find the transient times and to plot the error as a function of the time \(t\).
def compute_transient_and_errors(
t: np.ndarray, samples: np.ndarray, time_step: float = None
) -> tuple:
"""Computes the transient time at an accuracy +- time_step/2
and the errors for all transient times considered.
"""
t0 = t[0]
if time_step is None:
time_step = (t[-1] - t[0]) / 100
eps_list = []
B_mean = B_mean_fitting(t=t, samples=samples)
B_std = B_std_fitting(t=t, samples=samples)
while (t0 - t[0]) < (t[-1] - t[0]) / 2:
t_eps = t[t > t0]
samples_eps = samples[t > t0]
T = t_eps[-1] - t_eps[0]
eps_mean = 1 / (np.sqrt(2 * B_mean * T)) * samples_eps.std()
eps_std = 1 / np.sqrt(4 * B_std * T) * samples_eps.std()
eps_list.append(eps_mean * eps_std)
t0 += time_step
t_t = t[0] + np.argmin(eps_list) * time_step
return t_t, eps_list
Application
Let’s now apply the method to detect the warm-up period on the signal presented !
import pandas as pd
data = pd.read_csv("avbp_mmm.csv", sep=",")
t = data["atime"].to_numpy()
samples = data["T_min"].to_numpy()
t_t, eps_list = compute_transient_and_errors(t=t, samples=samples)
The output of this program can then be used to build the following plot:
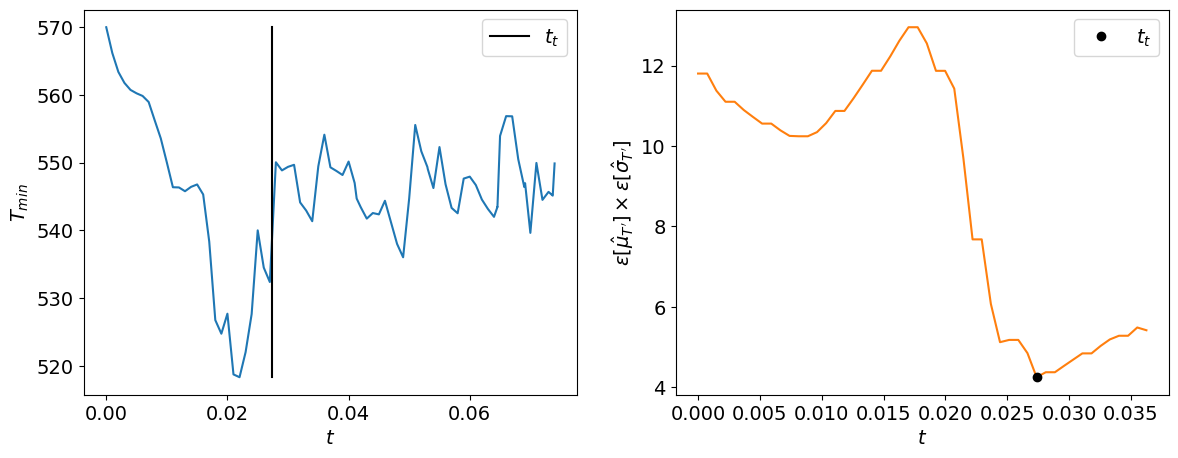
The transient time \(t_t\) detected with the method is coherent with the visual inspection of the signal (left on the figure). On the right of the figure, you can observe the total error as a function of the time. The minimum of this curve gives the transient time.
Reverse method
Note that this method can easily be extended to the case where you want to find the end of an initially steady state becoming unsteady (e.g. in an extinction simulation). The method is the same, except that this time we shorten the signal from the ending edge:
def compute_reverse_transient_and_errors(
t: np.ndarray, samples: np.ndarray, time_step: float = None
) -> tuple:
"""Computes the transient time from the end of the signal at an accuracy +- time_step/2
and the errors for all transient times considered.
"""
t0 = t[-1]
if time_step is None:
time_step = (t[-1] - t[0]) / 100
eps_list = []
B_mean = B_mean_fitting(t=t, samples=samples)
B_std = B_std_fitting(t=t, samples=samples)
while (t0 - t[0]) > (t[-1] - t[0]) / 2:
t_eps = t[t < t0]
samples_eps = samples[t < t0]
T = t_eps[-1] - t_eps[0]
eps_mean = 1 / (np.sqrt(2 * B_mean * T)) * samples_eps.std()
eps_std = 1 / np.sqrt(4 * B_std * T) * samples_eps.std()
eps_list.append(eps_mean * eps_std)
t0 -= time_step
t_t = t[-1] - np.argmin(eps_list) * time_step
return t_t, eps_list
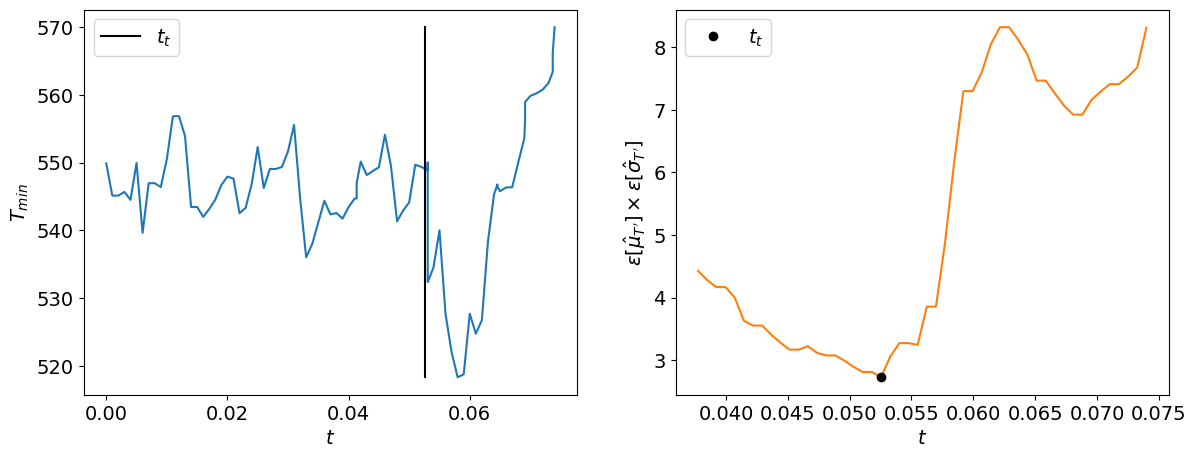
If we flip the original signal and we apply this function on the resulting signal, we obtain the following:
reverse_samples = np.flip(samples)
t_t, eps_list = compute_reverse_transient_and_errors(t=t, samples=reverse_samples)
Limitations
We observed however a limitation in this algorithm. Indeed, as said earlier, the warm-up period is supposed to distort the mean or standard deviation compared to the statistically steady state. However, if the signal of the warm-up period remains in the range of amplitudes of the signal of the statistically steady state, the algorithm will not detect the period change. The following examples show this limitation.
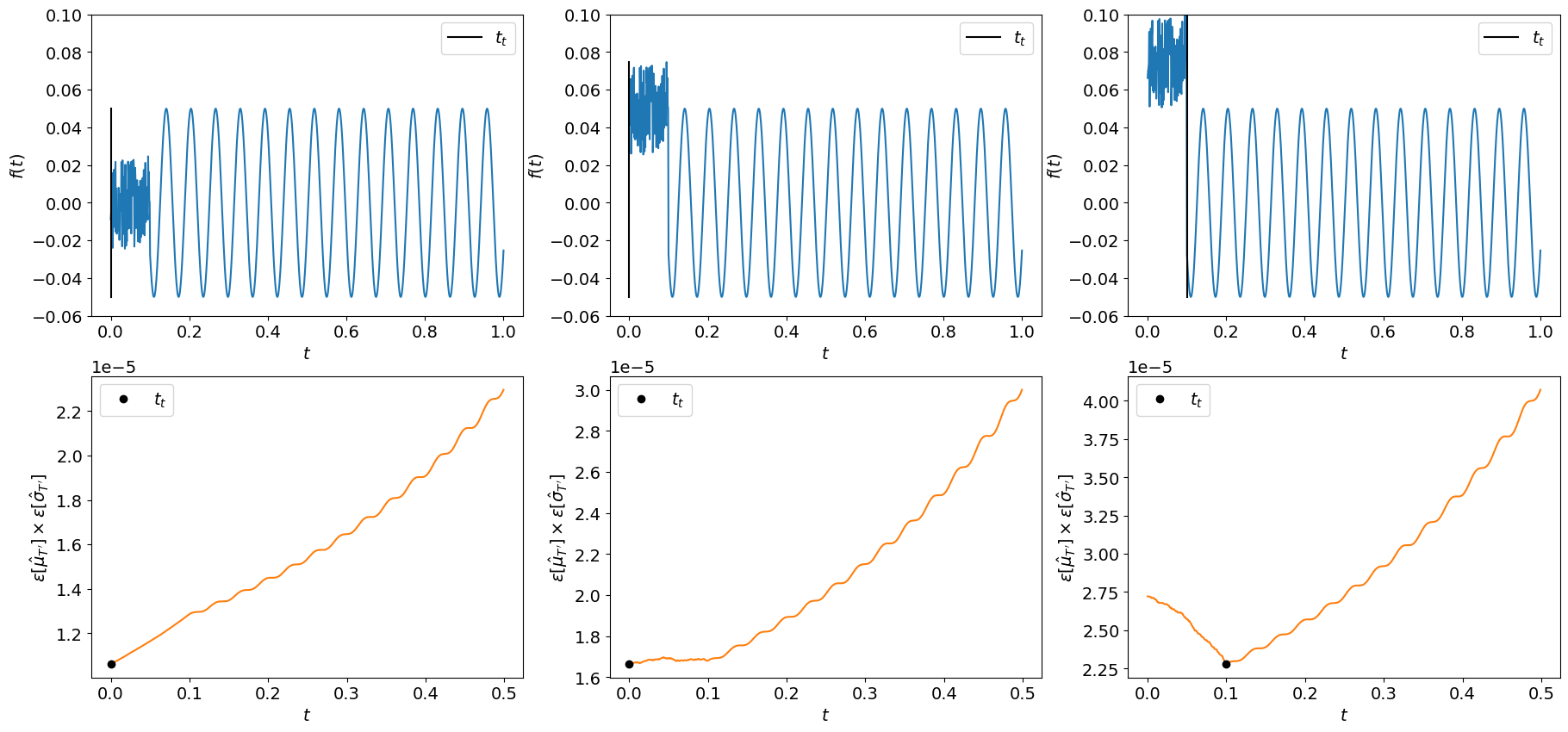
Takeaways
In this post, we were interested in detecting the warm-up period in a signal. Despite its limitations previously shown, the Python scripts presented here may help you in getting rid of this period in a signal and automate you post-treatment for reliable statistics.
The error formulas introduced may also be used to build a workflow that would run until the error on the statistics estimates reach a certain threshold or that we have an adequate confidence interval on the desired quantity.
Acknowledgements
Many thanks to Francesco Salvadore and Antonio Memmolo from CINECA for bringing this article to our attention through their initial FORTRAN implementation convdetect.This work is part of center of excellence EXCELLERAT Phase 2, funded by the European Union. This work has received funding from the European High Performance Computing Joint Undertaking (JU) and Germany, Italy, Slovenia, Spain, Sweden, and France under grant agreement No 101092621.

