L'algèbre linéaire numérique est au cœur de pratiquement toutes les applications en calcul scientifique. Elle fournit un cadre mathématique pour le traitement d'images ou de données géométriques, elle est à la base des méthodes numériques pour la solution d'équations différentielles ordinaires ou partielles, et elle est également devenue un outil central pour ce thème très en vogue qu'est le big data.
La relation profonde existant entre l'algèbre linéaire numérique et les équations aux dérivées partielles (EDP) ou ordinaires (EDO) ou reste cruciale en ingénierie et en science. A l'exception des cas où des méthodes explicites sont utilisées, la dicrétisation d'EDPs donne à résoudre des systèmes d'équations linéaires ou non-linéaires. Le cas non-linéaire requiert la solution répétée d'équations linéaires. Pour la plupart des équations et méthodes de discrétisation, les matrices des systèmes linéaires sont creuses. Le CERFACS a une expertise de plus de trente ans dans la résolution de systèmes de ce type, et est un centre de recherche internationalement reconnu comme l'un des leaders dans ce domaine. Durant la dernière décennie, la recherche s'est concentrée sur le développement de méthode directes présentant un grand potentiel de parallélisme. Plus récemment, le CERFACS s'intéresse à des solveurs itératifs hautements parallèles, et sur l'utilisation de méthodes hybrides afin d'étendre le potentiel des méthodes directes. En particulier, l'équipe Algo se concentre sur les méthodes multigrilles et multilevel qui sont parmi les candidats privilégiés afin d'atteindre la performance et la scalabilité nécessaires pour les futurs calculs exascale. Pour démontrer le potentiel d'application sur des problèmes ingénierie réels, nous avons testé ces méthodes pour la solutions de problèmes de très grande taille en collaboration avec nos partenaires académiques et industriels.
Quelques exemples de nos travaux de recherche récents:
Méthodes itératives, directes et hybrides directes-itératives
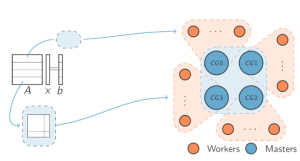Nous nous concentrons sur des problèmes centraux en algèbre linéaire numérique qui sont intéressants à la fois d'un point de vue académique et d'un point de vue applicatif pour le CERFACS et ses actionnaires. Par exemple, en collaboration avec notre partenaire industriel EDF, nous travaillons sur des méthodes pour la solution de systèmes linéaires provenant de l'analyse structurelle d'enceintes de confinement de réacteurs. Pour ces problèmes, le solveur itératif ainsi développé montre une excellente convergence en seulement quelques itérations [2]. Ce solveur a été intégré dans le code éléments finis d'EDF, code_aster, au travers d'une implémentation dans la librairie open source d'algèbre linéaire PETSc. Un exemple de notre travail de recherche académique est la thèse récemment soutenue de Philippe Leleux, sur les solveurs hybrides directs-itératifs pour les systèmes indéfinis et surdéterminés sur les futures architectures exascale, où l'accent a été mis sur les méthodes itératives et hybrides.
Méthodes multigrilles et multilevel
Les méthodes multigrilles sont parmi les seuls solveurs avec une complexité numérique linéaire et sont donc des candidats privilégiés pour exploiter pleinement le potentiel du calcul à des échelles extrêmes. Un des sujets de recherche actuels est le développement d'algorithmes de ce type, et des techniques permettant de les implémenter sur des architectures massivement parallèles et hétérogènes. L'équipe algo participe au projet H2020 Energy oriented Center of Excellence EoCoE 2. Dans ce cadre, un solveur multigrilles a été spécifiquement conçu pour la solution d'équation de Poisson gyrokinétiques sur des géométries circulaires décrites avec des coordonnées polaires. Cette algorithme a démontré un fort potentiel de scalabilité parallèle et, puisqu'il est basé sur une implémentation dite matrix-free, possède une très basse consommation en mémoire.
[1] Kuehn, M., Kruse, C., Ruede, U., Energy-minimizing, symmetric finite differences for anisotropic meshes and energy functional extrapolation, 2020, https://hal.archives-ouvertes.fr/hal-02941899/document
[2] Kruse, C., Darrigrand, V., Tardieu, N. et al. Application of an iterative Golub-Kahan algorithm to structural mechanics problems with multi-point constraints. Adv. Model. and Simul. in Eng. Sci. 7, 45 (2020). https://doi.org/10.1186/s40323-020-00181-2
