Type annotation with Python

Python typing system

Python is a dynamically typed langage as opposed to statically typed. This means that the Python interpreter does not necessarilly know the type of the objects before the actual code execution.

Dynamic typing is most of the time used in script languages such as Ruby, JavaScript, MATLAB or more than 90 other languages. On the other side of the spectrum, statically typed languages are often compiled instead of interpreted. Examples of statically typed langages include Fortran, C, C++ or Java.

Python being a dynamically typed language, the Python interpreter does not need to know the type of the manipulated objects before their initialisation. Thanks to this property, the following code snippet is considered valid.

def do_i_want_an_int():
    # Complex and long computations
    return computation_is_success

if do_i_want_an_int():
    a = 1
else:
    a = "I'm a string"

In this code snippet, the type of the object a depends on a value that can only be known at runtime, so the type is dynamically infered by the Python interpreter when the a object is created.

The dynamic nature of types in Python also allows Python functions parameters to accept any object no matter its type:

def f(obj):
    print(type(obj))

f(1)    # >>> <class 'int'>
f("a")  # >>> <class 'str'>
f(f)    # >>> <function f at 0x7f9045b64400>
f([])   # >>> <class 'list'>

Is dynamic typing good or bad?

There is no definitive answer to this question. Depending on the project and its goals, dynamically typed languages might or might not be the most appropriate tool to solve your problem.

In the special case of Python, dynamic typing means a lot of flexibility given to the programmer. But this flexibility comes with some drawbacks I will try to illustrate in the next few sections.

Type information is a form of documentation

Thanks to Python’s dynamic typing system, you do not need to write down types anymore. The following piece of code is perfectly valid:

def append_to_container(c, e):
    # Code of the function

Now ask yourself a simple question: are you able to infer with 100% certainty how to use this function without looking at its implementation?

Without any doubt the answer to the previous question is no. It is not possible to know with certainty how we should call this function without looking at its implementation. Not convinced? Here are two “valid” but incompatible ways of using this function

# First possibility
c = [1, 2]
e = 3
append_to_container(c, e)  # c is modified in-place in the function and the
                           # function does not return any value

# Second possibility
c = [1, 2]
e = 3
new_c = append_to_container(c, e)  # c is copied internally by the function and a modified
                                   # copy is returned.

It is impossible to guess from the signature of the append_to_container function which way is the correct one.

One possible solution would be to add documentation to the function with a docstring:

def append_to_container(c, e):
    """Modify c in-place to append e at the end of the container."""
    # Code of the function

But this leads to complications:

• Docstrings (and documentation is general) often end up being out of date because they are not changed along with the function evolution.
• Docstrings might be poorly written:

# Example of a useless docstring. The docstring only repeats informations 
# already present in the function or arguments names.
def append_to_container(c, e):
"""Append element e to the contained c."""
    # Code of the function

• Docstrings are not parsable by automated tools such as integrated development environments or code analysers, except if they adhere to very strict formatting rules (see Sphinx format, Google format or Numpy format).

Several IDE features are based on types

Being able to infer the type of variable allows IDE to include a lot of productivity-oriented features such as:

1. Displaying documentation in tooltips:

   

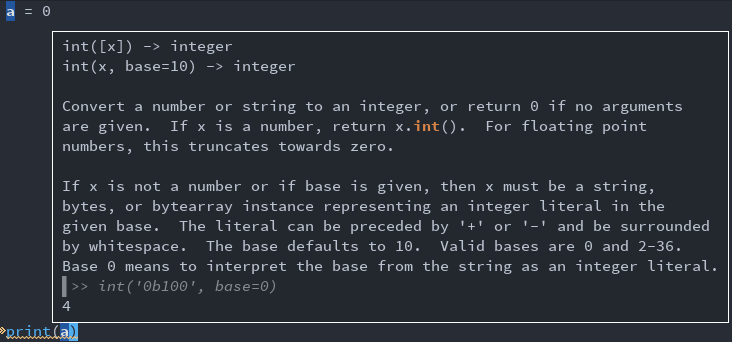
2. Displaying errors or warnings when the given type mismatch with the expected type:

   

3. “Go to type definition” is very usefull when exploring a new code base.

Type information allows more meaningful errors

Knowing what the type of a variable should be beforehand allows to check at runtime, when the variable is assigned, that the object assigned to the variable has the right type.

def count_bit_number(i):
    return i.bit_length()

a = count_bit_number(3)  # result is 2
b = count_bit_number(1.0)

The last line of the code snippet above raises the error:

AttributeError: 'float' object has no attribute 'bit_length'

where, if Python was aware that the function count_bit_number was only accepting integers as inputs, the error message could have been something like

TypeError: 'count_bit_number' got a 'float', expected 'int'

Improving Python with types

Because of all the reasons detailled in the previous section, people have been trying to add types to Python. But rather than changing the typing system of Python (which is a huge breaking change with a lot of implications) core Python developpers opted for type annotations.

Note that the word annotation has been chosen with care: all the type information are completely and simply discarded and not used by the Python interpreter. Rephrasing, type annotations have the exact same status as comments for the interpreter and are not processed in any way.

How to annotate in Python

Variables

Variables are annotated using the notation [variable identifier]: [type]. Several examples are given in the following code snippet.

i: int = 1
f: float = 1.0
s: str = "I am a string"
b: bool = False

# Note that the following line is accepted by the interpreter
not_string: string = 1
print(type(not_string))  # outputs "int"

Some Python structures do not allow including type annotations at the variable declaration. The for loop is an example, the with block is another. In order to circumvent this issue, you can “pre-declare” your variables with their type as follow:

i: int
for i in range(10):
    print(f"I am the number {i}!")

Function signatures

Function parameters are annotated just like variables, but within the function signature:

def add(lhs: int, rhs: int):
    return lhs + rhs

a = add(1, 2)
from math import pi
b = add(1.0, pi)  # Works as expected because types are not accounted for by the interpreter
print(b)  # Outputs "4.141592653589793"

A special syntax exists for return types: using -> [return type] just before the : at the end of the function signature:

def add(lhs: int, rhs: int) -> int:
    return lhs + rhs

More complex types

For the moment we limited ourselves to simple primitive types. But what about more complex, composite or user-defined types?

User-defined types works exactly the same way as primitive ones:

class MyVeryUsefulType:
    pass

def a_very_useful_function(a: MyVeryUsefulType) -> MyVeryUsefulType:
    return a

useless_instance: MyVeryUsefulType = MyVeryUsefulType()
a_very_useful_function(useless_instance)

But what if my type is a list of int? In this case, in order to represent the list of int type, Python 3.5 introduced a new package called typing.

from typing import List  # Note the upper-case letter

my_int_list: List[int] = []
list_of_list: List[List] = []  # Can be nested
multi_dimensional_complex: List[List[List[List[List[complex]]]]] = []  # can be nested a lot

The typing package includes a lot of pre-defined type annotation structures, some of the most important ones being:

1. Set for the set primitive type.
2. Tuple for the tuple primitive type.
3. Callable for anything that can be called as a function. This obviously includes functions, but also function objects or really anything that is… callable. The syntax to define the signature (parameter types and return type) of the callable is described in the typing documentation.
4. Sequence for containers that implement a given set of methods, see the Collection of Abstract Base Classes for a description.
5. Iterable for anything that implement the __iter__ method.
6. Any for any type.
7. Union, used to encode a logical OR between two or more types. Union[int, float] means that the expected type is one of int or float.

Coming back to our first example

We introduced an append_to_container function at the beginning of this post, lets modify its definition with the newly introduced typing annotations:

from typing import List, TypeVar

T = TypeVar("T")  # Generic type variable

def append_to_container(c: List[T], e: T) -> None:
    c.append(e)

In this code we first import the necessary definitions from the typing module. Then, we create a generic type variable, called T. This variable is a placeholder and its only purpose is to convey the information that the function append_to_container expects its first parameter to be a list of T and its second parameter to be an instance of the exact same type T, no matter the actual type T. Finally, the -> None explicitly means “this function is not supposed to return something”.

Thanks to the newly specified signature of append_to_container, it is now clear how to use the function. The first proposition, consisting in calling the function knowing that it will modify in-place the data structure provided, is the right one. Below are three examples that are compliant with the function annotations:

append_to_container([1.0], 2.0)
my_list = [True]
append_to_container(my_list, False)
# Motivational example from the beginning
c = [1, 2]
e = 3
append_to_container(c, e)  # c is modified in-place in the function and the
                           # function does not return any value

Remember that typing annotations are annotations. As such, it is still possible to call the add_to_container function with arguments that do not comply with the type annotations provided. If the operations performed in the function are meaningful with the provided types, the function will not throw. Below is an example with a list instead of an int:

my_int_list = [4]
append_to_container(my_int_list, [2])
print(my_int_list)

Interesting reads:

• PEP 484 that introduced the type-annotation syntax and the typing package in Python.
• Our journey to type checking 4 million lines of Python: a blog post written by the initiator of type-annotation in Python and now working at Dropbox that explains very nicely why and how Dropbox quickly adopted type annotation.
• Documentation of the typing module.

Like this post? Share on: Twitter ❄ Facebook ❄ Email