🎓Soutenance de thèse Markus HOLZER
Vendredi 29 novembre 2024Du 14h30 à 16h30
Thèses Cerfacs FAU Allemagne
Génération de code automatique pour le calcul exaflopique pour la méthode de Boltzmann sur réseaux
Ecole doctorale 475 Mathématiques, Informatique et Télécommunications de Toulouse (EDMITT)
https://fau.zoom-x.de/j/97059928526?pwd=L2hmVHJoSjg5SHd4YiswOUV2OFZUdz09
Les superordinateurs Exascale sont des systèmes informatiques capables de réaliser 1e18 opérations en virgule flottante par seconde, appellé un exaFLOPS. Le superordinateur Frontier a franchi pour la première fois la barrière d'un exaFLOPS et a officiellement ouvert l'ère du calcul exascale en 2022. L'immense échelle de systèmes tels que celui-ci impose des défis importants dans le développement de codes capables d'exploiter pleinement cette puissance de calcul. En outre, le matériel de plus en plus hétérogène utilisé par les principaux superordinateurs d'aujourd'hui ajoute une couche supplémentaire de complexité. Dans le domaine de la mécanique des fluides numérique, il est donc crucial d'examiner soigneusement chaque aspect d'une simulation numérique, en commençant par la conception et la sélection d'algorithmes adaptés à de tels environnements. Par exemple, des algorithmes tels que méthode de Boltzmann sont explicitement conçus avec un parallélisme massif à l'esprit, ce qui en fait une alternative notable à d'autres méthodes plus établies. Néanmoins, une mise en œuvre très efficace de cet algorithme doit être adaptée au matériel respectif pour une utilisation optimale des ressources.
Pour relever ces défis, cette thèse explore l'utilisation de la génération de code par le biais d'un langage intégré spécifique à un domaine. La génération de code nous permet de cibler des architectures matérielles spécifiques et d'appliquer des optimisations précises qui exploitent les connaissances spécifiques au domaine. Dans le cadre de cette recherche, nous étendons et remanions le paquet Python lbmpy pour prendre en charge les variantes de pointe de la méthode de Boltzmann. lbmpy représente la méthode de Boltzmann symboliquement en utilisant un système d'algèbre informatique, permettant la dérivation automatique d'équations discrétisées basées sur des spécifications définies par l'utilisateur. Pour obtenir des équations avec un minimum d'opérations en virgule flottante, nous améliorons fondamentalement les capacités de simplification de lbmpy dans ce travail. Les équations discrétisées dérivées par lbmpy sont fournies au paquet Python pystencils qui génère des noyaux de calcul spécifiques à l'architecture hautement optimisés dans un langage de niveau inférieur à partir de celles-ci. Nous élargissons la gamme des plates-formes matérielles prises en charge et révisons des aspects cruciaux du processus de génération de code, tels que le système de typage, afin d'améliorer les performances et la maintenabilité.
Une intégration sophistiquée de ces noyaux de calcul dans le cadre multiphysique massivement parallèle waLBerla est également développée, avec une discussion approfondie des composants clés de la mise en œuvre. L'une des avancées les plus significatives de cette intégration est la génération de noyaux d'interpolation hautement spécialisés. Ces noyaux sont essentiels pour le transfert d'informations entre des cellules de résolutions différentes au sein du domaine de simulation, garantissant la précision et la cohérence des données sur des grilles de tailles différentes. Ce développement nous a permis d'effectuer la plus grande simulation à ce jour en utilisant la méthode de Boltzmann sur un domaine non uniforme, en utilisant plus de 4000 AMD MI250X processeur graphique. La capacité à gérer efficacement un environnement de calcul aussi vaste et hétérogène souligne l'efficacité de notre approche dans la mise à l'échelle de simulations complexes sur des plates-formes matérielles de nouvelle génération.
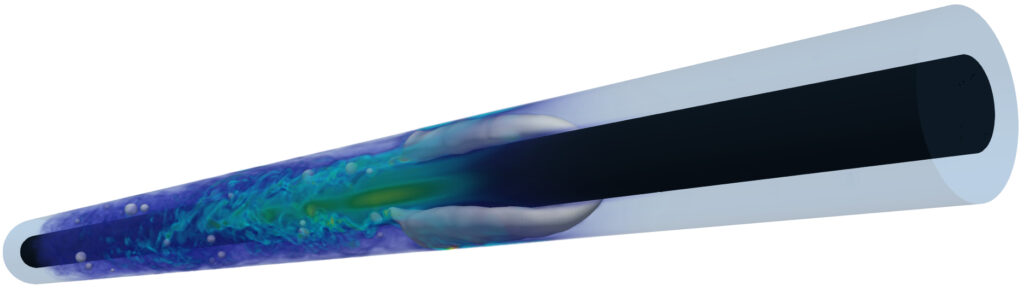
Nous vérifions et validons notre approche en simulant un écoulement monophasique turbulent autour d'une sphère à l'aide d'une configuration de maillage non uniforme sur processeurs graphiques, reproduisant avec succès la crise de traînée – un phénomène complexe qui se produit à des nombres de Reynolds supérieurs à 200 000. En outre, nous démontrons les capacités de notre méthode par le biais de simulations d'écoulements de boue, offrant de nouvelles perspectives sur le comportement des bulles de Taylor dans des configurations de tuyaux annulaires complexes. Enfin, nous analysons les trajectoires des gouttelettes sous l'influence d'une source de chaleur laser dans des écoulements thermocapillaires tridimensionnels. Pour évaluer les performances de notre approche, nous présentons les résultats de tous ces scénarios sur les processeurs et processeurs graphiques les plus récent. Nous fournissons des données de performance pour un seul nœud et offrons des informations précieuses en contextualisant les résultats mesurés avec des modèles de performance appropriés. Enfin, nous examinons l'évolutivité de nos développements en présentant des résultats d'évolutivité faibles et forts sur plusieurs des principaux superordinateurs du monde.
JURY
| Jonas LATT | Université de Genève | Rapporteur |
| Christian HOLM | Université de Stuttgart | Rapporteur |
| Ulrich RÜDE | FAU / CERFACS | Rapporteur / Directeur de thèse |
| Jens HARTING | FZ-Jülich | Examinateur |
| Tobias GÜNTER | FAU | Président du Jury |
| Eric CLIMENT | IMFT | Examinateur |
| Gabriel STAFFELBACH | ONERA | Co-directeur de thèse |
| Catherine LAMBERT | CERFACS | Directrice de thèse |
No content defined in the sidebar.

