Numerical Methods for CFD

Effects of numerical schemes

Mesh and discretization 

This document is devoted to the discretization of the Navier-Stokes equations. After introducing the notations, the meshes needed to discretize the equations are presented, with theirs pro and cons. Finally, the last chapter makes a link between meshes and data location within the mesh. The analysis is done for both codes used at CERFACS (ABVP and elsA).

Stability, dispersion and dissipation 

Computational Fluid Dynamics is the ability of simulating complex flow features by use of computers when analytical solutions are not accessible which is the case for a lot of flow problems. Since computers can only produce a set of mathematical operations (addition, substraction, multiplication, division and logical operations) to be operated on discrete numbers of various types (booleans, integer, real, double...), the notion of discretization is needed to transform the original governing equations. Different procedures can be employed to transform the evolution equations into a set of discrete values onto which operations can be applied by the computer. However all of these schemes suffer from the same problems that any CFD specialist is supposed to handle before addressing any type of simulation by use of a commercial or preferred Fortran/C++ code.

The aim of this lecture is thus to illustrate and introduce readers to the notion of:

• Stability: the ability of a discretization to produce approximations that are bounded or why does my code sometimes gives me nice numbers and others NAN’s (Not A Number) in my solution file?
• Dispersion and Dissipation: the ability or inability for a discretization to at- tenuate oscillations or scramble a nice and continuous signal.

Convection Scheme 

The Euler's equations are the model problem for the establishment and the analysis of numerical schemes devoted to convection flux integrals. The analysis of the Euler equations will be the basis of the above document.

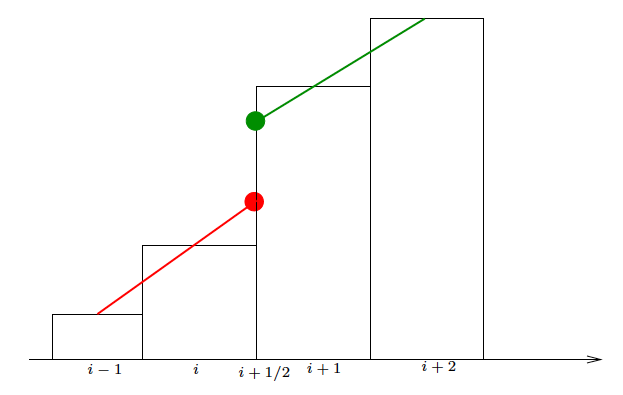
Illustration: the first order extrapolation for the decentered formulation.

Benchmarks 

Friction channel test-case for LES codes using wall-laws 

The aim of this test case is to compare the performances of numerical simulations performed with various LES codes. It is open to anyone interested in evaluating their LES code on a simple friction test case. The configuration is a bi-periodic turbulent channel with isothermal walls. Wall treatment is done using wall laws. Two meshes are suggested for the study, aiming for two values of y+ which depend on the numerical methods (cell-centered, node-centered...) but in the order of 50 to 200 in order for the wall-law to apply. The friction Reynolds number is set to 2003, and the expected velocity profiles are those of the DNS by Alamo and Jiménez. Velocity profile comparisons including rms values should give an excellent view of the quality of the numerical methods in reproducing the correct turbulent parameters under friction.

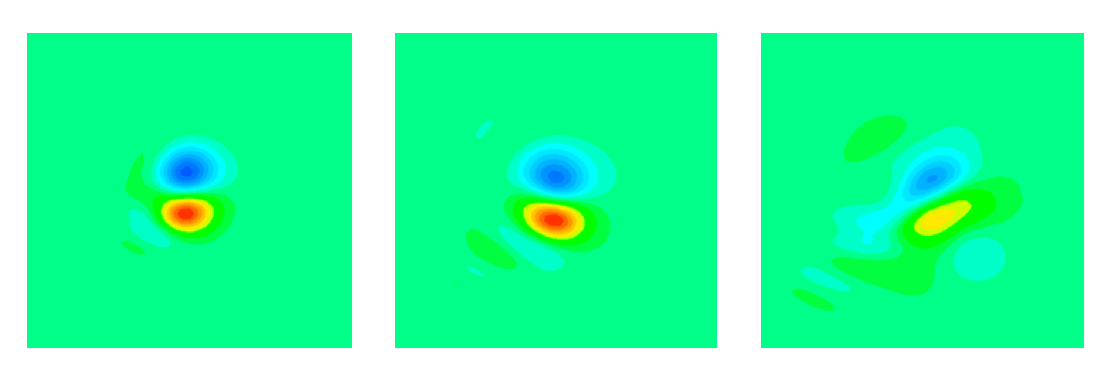
Illustration : CO-VO test-cas, dissipation  of the vortex.

CO-VO test-case for DNS/LES codes   

This site is a platform open to all groups interested in comparing their DNS/LES codes on a very simple case: the convection of a vortex on a mean, constant speed flow. It represents the simplest prototype of what high fidelity codes must do in DNS or LES: convect vortices over long distances at the right speed and the right amplitude. The computation is performed without viscosity and the expected solution is simply the initial vortex convected without deformation. The computation is performed in a periodic box in which the vortex turns for 10, 20, 30 and 40 turn over times. Comparing the solution at these instants with the initial solution is an excellent qualification of the solvers accuracy. A small grid (80 by 80) is used for accuracy while a three dimensional grid is used to measure speed and efficiency on parallel machines.

VW test-case for DNS/LES codes  

This test-case open to all groups interested in comparing their DNS/LES codes on a very simple configuration: the interaction of a pair of vortex with a wall.

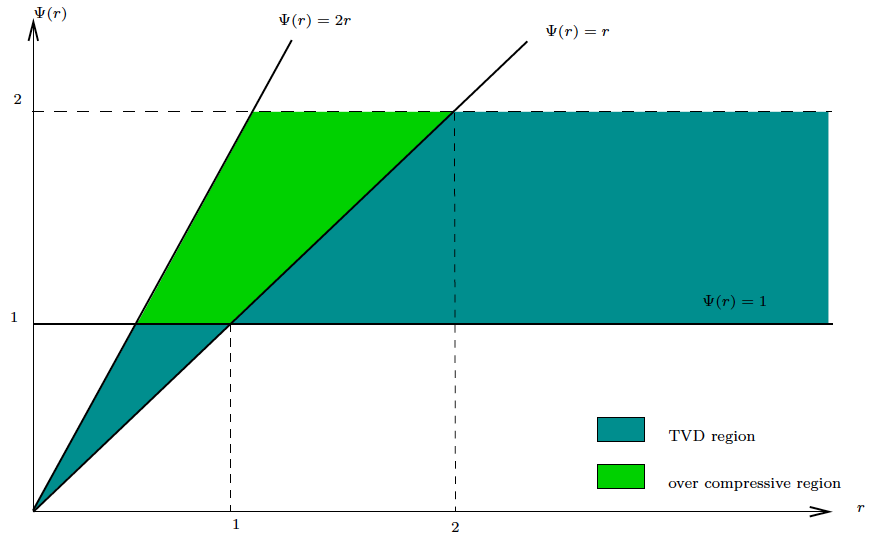
Illustration: definition of the TVD region.

Published on  March 2nd, 2023