Environment Science

Principles of hydraulic

This courses was given at the french École Polytechnique.

Incompressible flows 

This chapter gives a summary of the essential steps of continuum mechanics which are needed to establish the incompressible Navier-Stokes equations. These equations come from the following ingredients:

• the axioms of mechanics : mass and momentum conservation,
• the incompressibility constraint,
• the rheologic constitutive law of Newtonian fluids.

We try to explicit all the above concepts in the simplest manner as possible. Readers who already knows “continuum mechanics” will only have to acknowledge the set of notations before studying the examples developed at the end of the chapter.

In the last sections of this chapter, two examples of flows are presented. Beyond their interest as applications examples of the incompressible Navier-Stokes equations, these flows are here used to introduce the hydraulics of flows in pipes and the hydraulics of free surface flows in open channel flows. In both examples the important concept of “hydraulic head” is introduced. The relation between the “lineic head loss” and the “shear stress” due to the boundaries is put forward.

The first example, which introduces flows in pipes, is the circular Poiseuille in a pipe, forced by a pressure gradient. When the flow is slow enough, it is laminar and its mean velocity is proportional to the lineic head loss. This important property is at the root of the Darcy law which is valid for flows in porous media such as, for example, the subsurface flows.

The second example, which introduces free surface flows, is the plane Poiseuille flow in an open tilted channel. One introduces the friction coefficient which comes out of a dimensional analysis on the head loss. When the flow becomes turbulent, which is the case for realistic open channel flows, the parametrization of this friction coefficient is at the center of the modelling of these flows.

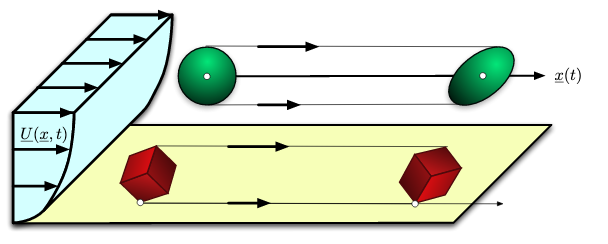
Illustration: articules motions in a parallel shear flow.

Potential flows 

The underground is made of a mix of earth and rock through which water infiltrates and circulates. This circulation is modelled by potential flows in a porous medium. These flows, which velocity field is the gradient of a potential, are encountered in fluid mechanics when the vorticity (curl of the velocity) can be neglected. This is the case of slow subsurface flows at scales which are large in front of the size of the gravels.

Basic notions of ground water hydraulics are presented in this chapter with the help of simple examples which are representative of more complex subsurface problems. Only slow flows, that is with low Reynolds numbers, in isotropic and homogeneous porous media are considered.

The hydraulic head of porous media is presented with the Bernoulli equation derived out the laminar Navier-Stokes equations. Since the velocity of flows in water media is small, the hydraulic head is approximated by the piezometric height. The Darcy law, which postulate a linear relation between the discharge velocity and the head loss, is presented on the simple example of the confined aquifer flowing in a single direction. The generalization of the Darcy law to three dimensional flows in homogeneous porous media shows that the head can be viewed as the potential of the discharge velocity. By applying the mass conservation, one shows that the head loss satisfies the Laplace equation.

Understanding the nature of the boundary conditions used to solve this Laplace equation is one of the key points of this chapter. Several examples are presented.

Turbulence and friction 

The goal of this chapter is to give an overview of the turbulence models which describe, from the engineering point of view, the friction of a walls on a flow.

This presentation of turbulence modelling is oriented towards the introduction of the empiric relations which express the turbulent friction coefficients as a function of global parameters of the flow, such as the average velocity and the section of the pipe (hydraulics in closed ducts) or the channel (open channel flows).

Simple notions on the decomposition between mean fields and turbulent fluctuations are given. By taking the average of transport equations or of the Navier-Stokes equations, the notions of turbulent fluxes and turbulence diffusivity are introduced. The mixing length model, which is helpful in a lot of engineering applications dealing with fluid mechanics, is explicited.

In the vicinity of a wall, such as the bottom of a channel flow or the inside boundaries of a pipe, the mixing length is the product of the distance to the wall and the Von Karman constant which value comes out of experiments. This robust law lead to identification of logarithm profiles for the velocity in the vicinity of the wall. The cases of smooth or rough boundaries are compared. They are limit cases of the “Moody diagram” which plot, for general roughnesses, the turbulent friction coefficient as a function of the Reynolds number and the dimensionless roughness.

Illustration: the Garonne in floods - Photo CNRS.

Fluvial hydraulic

Open channel flows 

The objective of this chapter is to present the basic models which describe open channel flows. Such flows are “gradually varied” the size of these sections are small compared to the chararcteristic scales of variation of their slope. We only consider here stationary flows under the “gradual variation” hypothesis.

The concept of “hydraulic head” for open channel flow is presented on the Bernoulli equation derived from the Navier-Stokes equations. The equation for the hydraulic head along the channel in the stationary case is written and applied to the case of a flow over an obstacle when the friction can be neglected. The concepts of “super-critical” and “sub-critical” flows, depending on the Froude number, are presented of this example.

Considerations on boundary conditions explain the advent of hydraulic jumps. The discontinuity equations for these hydraulic jumps are presented in a simple manner. The turbulent friction of the bottom on the channel is modelled through a Manning-Strickler parametrization, which is very common for open channel flow engineer approach. The description of the “back water curves” is given in the case of this parametrization and the notions of “normal height” and “critical height” are used to classify these curves.

Flood waves 

Open channel flows often come in the investigation and intervention scope of the environment engineer. Very often, the water layer depth is weak compared to the horizontal extension of the observed phenomena. This is the case for flows in rivers or channels and of the ground runoff.

One restrains here to channels which section is a rectangle of top width L large compared to the depth, but the generalization to channels with variable sections can be done without difficulties.

The transition from turbulent Navier-Stokes equations is tackled by using the Leibnitz formula. A series of approximations allowing to neglect one or several terms of the Saint-Venant equations is presented.

The kinematic flood wave approximation is then used for its hydraulic rele- vance and its simplicity in the illustration of the method of characteristics. The exemple of the expansion wave eases the understanding of the notion of invariant carried by the characteristic velocity. The computation of the propagation velocity of a shock from the global formulation of the model is explicited.

Published on  September 30th, 2020