Azimuthal Average¶
Description¶
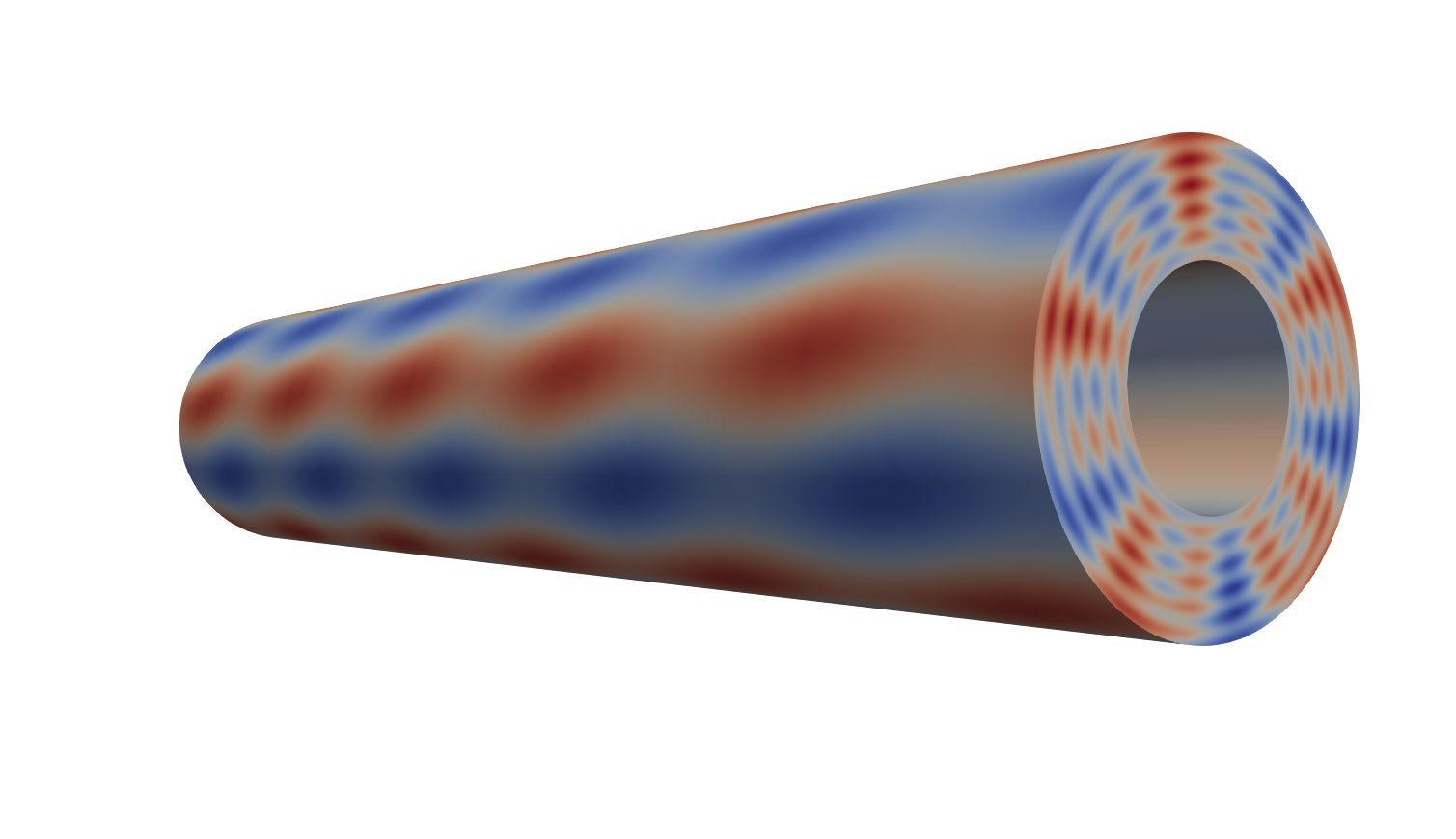
Azimuthal averaging around a given axis of a single-zone base.
3D axisymmetric mesh on the left. 2D meridional mesh on the right resulting from the azimuthal average.
This treatment spawns multiple processes thanks to the multiprocessing package.
A number of azimuthal slices are interpolated on a reference slice.
Parameters¶
- base:
Base The single-zone input base.
- base:
- axis: list(float)
The Cartesian coordinates of the revolution unit axis of the averaging. Valid values are [1., 0., 0.] or [0., 1., 0.] or [0., 0., 1.].
- origin: list(float)
The Cartesian coordinates (list of 3 floats) of the origin of the cylindrical coordinate system.
- nb_cuts: int
The desired number of azimuthal slices for the averaging. This gives a uniform discretization of the azimuthal direction.
- nb_procs: int
The desired number of processes used to perform the averaging.
- type: str, default= ‘Full’
The type of averaging needed. The values are:
‘Full’ for a 360 degree average
‘Sector’
If ‘Sector’ is selected, the user must enter the angles values.
- angles: list(float), default= [0, pi]
Angles (in radian) defining the averaging sector.
example: treatment[‘angles’] = [0, pi/2] will perform the averaging between 0 and pi/2.
The angles are defined differently depending on the axis:
if axis = [1,0,0] ; angle=0 lies on y-axis while angle=pi/2 lies on z-axis
if axis = [0,1,0] ; angle=0 lies on z-axis while angle=pi/2 lies on x-axis
if axis = [0,0,1] ; angle=0 lies on x-axis while angle=pi/2 lies on y-axis
- vector: list(str), default= None
List of 3 strings denoting the name of the X, Y, Z components of the vector in the Cartesian coordinate system. The order is important. This vector will be transformed into cylindrical coordinates during the azimuthal averaging procedure.
- matrix: list(str), default= None
List of 6 strings denoting the name of the XX, XY, XZ, YY, YZ, ZZ components of the matrix in the Cartesian coordinate system. The order is important. This matrix will be transformed into cylindrical coordinates during the azimuthal averaging procedure.
- duplicate: bool, default= False
If True, and if type = ‘Full’, it duplicates the fields and paste it on the other side of the axis of rotation. Can be useful (esthetically) for symetric plots or colormaps.
- multithreading: bool, default= False
If True, the treatment will use a more memory efficient method to compute the azimuthal average. It will take longer in average, but can be useful when the script is restricted in memory. You need to install Antares with –mshcppcutter and the right flags for this option to work. nb_procs will become the number of threads used for each cut.
- cut_type: str, default= “cut”
The cut treatment to use. By default, uses VTK’s cut. Valid options are “cut” for
antares.treatment.TreatmentCut.TreatmentCut, “acut” forantares.treatment.TreatmentAcut.TreatmentAcut, and “ccut” forantares.treatment.TreatmentCcut.TreatmentCcut.
Preconditions¶
The input base must contain only one zone. The coordinates must be (at least) in the first instant.
Requirements for averaging type:
Full: ‘axis’, ‘origin’, ‘nb_cuts’, ‘nb_procs’
Sector: ‘axis’, ‘origin’, ‘nb_cuts’, ‘nb_procs’, ‘angles’
Postconditions¶
Example¶
The following example shows an azimuthal average around the axis (1., 0., 0.) using (0., 0., 0.) as origin. The average is performed over 360 degrees (‘Full’ selected)
import antares
myt = antares.Treatment('AzimuthalAverage')
myt['base'] = base
myt['type'] = 'Full'
myt['origin'] = [0., 0., 0.]
myt['axis'] = [1., 0., 0.]
myt['nb_procs'] = 10
myt['nb_cuts'] = 180
cutbase = myt.execute()