Chorochronic Reconstruction (Asynchronous)¶
Description¶
Compute the chorochronic (or multi-chorochronic) reconstruction of a CFD computation for asynchronous phenomenon.
Here is given an example of the classic chorochronic reconstruction (only two rows and one resolved frequency per row). The same principles apply for the multi-chorochronic reconstruction (more than two rows and multiple frequencies resolved per row).
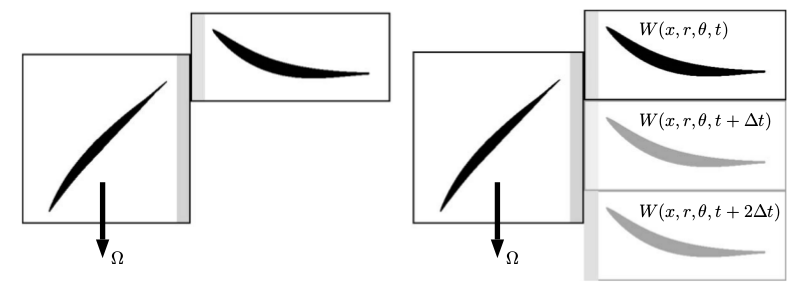
On the left, relative mesh position of two blade rows. On the right, duplication with phase-lagged periodic conditions.
When solving for only one blade passage of the real geometry, the flow is time-lagged from one blade passage to another. The phase-lagged periodic condition is used on the azimuthal boundaries of a single blade passage. It states that the flow in a blade passage at time t is the flow at the next passage, but at another time \(t + \Delta t\): \(W(x, r, \theta + \theta_p, t) = W(x, r, \theta, t + \Delta t)\).
This time lag can be expressed as the phase of a rotating wave traveling at the same speed as the relative rotation speed of the opposite row: \(\Delta t = \beta/\omega_\beta\). The interblade phase angle \(\beta\) depends on each row blade number and relative rotation velocity: \(\beta = 2 \pi sgn(\omega_r-\omega_s) (1-N_s/N_r)\).
The Fourier series (of the above flow equation) are: \(\sum_{k=-\infty}^{k=\infty} \hat{W_k}(x, r, \theta + \theta_p) \exp(i k \omega_\beta t) = \sum_{k=-\infty}^{k=\infty} \hat{W_k}(x, r, \theta) \exp(i k \omega_\beta t) \exp(i k \omega_\beta \Delta t)\). The spectrum of the flow is then equal to the spectrum of the neighbor blade passage modulated by a complex exponential depending on the interblade phase angle: \(\hat{W_k}(x, r, \theta + \theta_p) = \hat{W_k}(x, r, \theta) \exp(i k \omega_\beta \Delta t)\).
This last relation is used to reconstruct the flow over time on several blade passages.
This treatment has two possibilities for flow reconstruction with partial information. One very efficient is the ‘least_square’ and is doing a least square optimization to compute fourier coefficient. The other one is the ‘shape_correction’ and is usually used during cfd computation to update coefficient
References¶
Aerodynamique 3D instationnaire des turbomachines axiales multi-etage, Julien Neubauer, PhD thesis, 2004 (link)
Evaluation of unsteady CFD models applied to the analysis of a transonic HP turbine stage, M. Giovannini & al., ETC10, 2013
Method of Simulating Unsteady Turbomachinery Flows with Multiple Perturbations, He, L., AIAA J., Vol. 30, 1992, pp. 2730{2735)
Parameters¶
- base:
Base The input base that will be chorochronically duplicated.
- base:
- type: str, default= ‘fourier’
The type of approach (‘fourier’ or ‘least_squares’) used to determine the amplitudes and phases of each interaction mode. If ‘least_squares’, a least-squares approach is used. For robustness and accuracy reasons, it is advised to have enough instants in the base to cover at least three oscillations ‘shape_correction’ is an online algorithm and converge slowly.
- coordinates: list(str)
The variable names that define the set of coordinates used for duplication. It is assumed that these are in cartesian coordinates.
- vectors: list(tuple(str), default= []
If the base contains vectors, these must be rotated. It is assumed that they are expressed in cartesian coordinates.
- reconstructed_ite: list(int), default= [0]
List of iterations to be reconstructed.
- nb_blade: int or ‘in_attr’, default= ‘in_attr’
Number of blades of the current row. If ‘in_attr’, then each zone of the base must have an attribute ‘nb_blade’.
- omega: float or ‘in_attr’, default= ‘in_attr’
Rotation speed of the current row expressed in radians per second. If ‘in_attr’, then each zone of the base must have an attribute ‘omega’.
- waves_freq: float or list(float) or ‘in_attr’, default= ‘in_attr’
Frequency simulated in the current row (or list of frequencies in the current row in the case of multiple rotating wave phenomenon) expressed in Hz. If ‘in_attr’, then each zone of the base must have an attribute ‘freq_of_interest’.
- waves_omega: float or list(float) or ‘in_attr’, default= ‘in_attr’
Rotation speed of the wave (or list of rotation speeds of the waves in the case of multiple rotating wave phenomenon) expressed in radians per second. If ‘in_attr’, then each zone of the base must have an attribute ‘wave_omega’.
- waves_nb_harm: int or list(int) or ‘in_attr’, default= None
Number of harmonics used for the reconstruction of waves. If not given, all the harmonics are computed for type ‘fourier’ and the first three harmonics are computed for type ‘least_squares’. If ‘in_attr’, then each zone of the base must have an attribute ‘wave_nb_harm.
- extracts_step: int, default= 1
The number of time iterations between two instants of the base. This number is assumed constant over pairs of successive instants.
- nb_duplication: int or tuple(int) or ‘in_attr’, default= ‘in_attr’
Number of duplications if an integer is given (given base included). Range of duplications if a tuple is given (from first element to second element included). If ‘in_attr’, then each zone of the base must have an attribute ‘nb_duplication’.
- ite_init: int, default= 0
Iteration of the first instant of the base.
- theta_init: float, default= None
Initial rotation of the first instant of the base. If not prescribed theta_init will be infered from ite_init while assuming timestep has been kept constant during the simulation.
- timestep: float, default= 1.0e-8
Constant time interval used during the simulation.