Instant

Container of numpy arrays.

An instant object is a collection of numpy arrays.

It contains several variables that can be located at the center of the geometrical element (cell), at the node, at the interfaces, or at a mix of cells and interfaces: cellfict.

From Python 3.7, python dictionaries store key-value pairs in the order they were inserted. They are insertion ordered.

The parent class UserDict acts as a wrapper around dictionary objects. This class can be easier to work with because the underlying dictionary is accessible as an attribute.

The alternative would be to use a MutableMapping that defines the interface, but we would need to store the data explicitely.

class antares.api.Instant.Instant(instant=None, connectivity=False, inherit_computer=None)

Indexed and insertion ordered dictionary of numpy arrays.

Contains several variables that can be located at the center of the cells or at the node.

Keys are of the form: (‘name of variables’, location).

Return keys as a list and not KeysView nor dict_keys.

Methods

add_computer_function(new_func)	Setter of the function.
are_all_shared(variables)	Check if variables are all shared.
cell_shape()	Get the cell shape of the instant.
clear()
closest(value, variables)	Get the closest indices to the values for the given variables.
compute(var_name[, location, reset, store])	Compute a given variable for the instant.
compute_cell_volume([coordinates])	Compute the volume of the cells.
compute_coordinate_system([ttype, ...])	Compute a new coordinate system in the instant.
copy()
delete_variables(list_vars[, location])	Delete variables in the instant.
deserialized(pickable_instant)	Build an instant from its representation.
dimension()	Return the dimension.
duplicate_variables(list_vars, list_newvars)	Duplicate variables in the instant.
fromkeys(iterable[, value])
get(k[,d])
get_celltype(celltype)	Return the subset of the instant with only a given element type.
get_location(location)	Return a copy of the Instant containing only the variables located in the original Instant at the specified location.
is_structured()	Tell whether the instant is structured or not.
is_unstructured()	Tells whether the instant is unstructured or not.
items()
keys([location, with_shared])	Get the list of all variable names.
mesh_orientation(coordinate_names)	Give the orientation of a 3D structured mesh.
node_to_cell([variables, with_shared])	Compute variables at cell centers from values given at nodes.
pop(k[,d])	If key is not found, d is returned if given, otherwise KeyError is raised.
popitem()	as a 2-tuple; but raise KeyError if D is empty.
rel_to_abs([coordinates, conservative_vars, ...])	Transform conservative variables in the instant from relative frame to absolute frame.
rename_variables(list_vars, list_newvars[, ...])	Rename variables in the instant.
serialized([data])	Build a pickable representation of the instant.
set_computer_model(modeling[, ...])	Setter of the computer.
set_formula(formula)	Setter of the formula.
setdefault(k[,d])
update([E, ]**F)	If E present and has a .keys() method, does: for k in E: D[k] = E[k] If E present and lacks .keys() method, does: for (k, v) in E: D[k] = v In either case, this is followed by: for k, v in F.items(): D[k] = v
values()

Attributes

attrs	Get the attributes of the Instant.
computer	Get the computer.
connectivity	Get the connectivities for unstructured grid.
shape	Get the shape of the Instant.

add_computer_function(new_func)

Setter of the function.

Parameters:

new_func (func) – a python function.

are_all_shared(variables)

Check if variables are all shared.

Parameters:

variables (list(str), or list(tuple(str)). e.g.: ['x', 'y'] or [('x','node'), ('y','cell')]) – Variable names.

Returns:

says if all the variables passed as parameters are shared

Return type:

bool

cell_shape()

Get the cell shape of the instant.

Returns:

the shape of the cell-centered variables

Return type:

int or ndarray(int)

closest(value, variables)

Get the closest indices to the values for the given variables.

Parameters:

• value (list of floats) – values to be close to

• variables (list(str)) – variables scanned

Returns:

index and distance of the closest point

Return type:

(tuple of integer, real)

compute(var_name, location=None, reset=False, store=True)

Compute a given variable for the instant.

This variable is computed with variables available in the instant.

Parameters:

• var_name (str) – The name of the variable to compute.

• location (str in LOCATIONS) – The location of the variable. If None, the default location is assumed.

• reset (bool) – Remove temporary fields stored in the equation manager.

• store (bool) – Store temporary fields in the equation manager.

compute_cell_volume(coordinates=['x', 'y', 'z'])

Compute the volume of the cells.

It is stored with the variable name (‘cell_volume’, ‘cell’).

Parameters:

coordinates (list(str)) – list of coordinate names

compute_coordinate_system(ttype='cartesian2cylindrical', remove_actual=False, actual_coord_sys=['x', 'y', 'z'], new_coord_sys=['x', 'r', 'theta'], origin=[0.0, 0.0, 0.0])

Compute a new coordinate system in the instant.

name DEFAULT_CARTESIAN_COORDINATES name DEFAULT_CYLINDRICAL_COORDINATES

Parameters:

• ttype (str in ['cartesian2cylindrical', 'cylindrical2cartesian']) – type of transformation

• remove_actual (bool) – remove actual coordinate system after transformation

• actual_coord_sys (list of 3 str) – names of the current coordinates

• new_coord_sys (list of 3 str) – names of the new coordinates

• origin (list of 3 float) – position of the origin

Warning

‘cylindrical2cartesian’ with non zero origin not implemented

for ‘ttype’=’cartesian2cylindrical’, in ‘new_coord_sys’, the first coordinate is the axial direction, the second the radial one, and the third the azimuthal one (by default (x, r, \(\theta\)))

The first coordinate name in ‘new_coord_sys’ must also be into ‘actual_coord_sys’.

delete_variables(list_vars, location=None)

Delete variables in the instant.

Parameters:

• list_vars (list(str)) – list of variables to delete

• location (str in LOCATIONS or ‘None’) – if None, delete the variables at all locations

classmethod deserialized(pickable_instant)

Build an instant from its representation.

dimension()

Return the dimension.

Returns:

dimension of the Instant

Return type:

int

duplicate_variables(list_vars, list_newvars, location=None)

Duplicate variables in the instant.

Parameters:

• list_vars (list(str)) – list of variables to duplicate

• list_newvars (list(str)) – list of new variable names

• location (str in LOCATIONS) – if different from None, change only the variables at the location specified

Duplication is performed element-wise.

get(k[, d]) → D[k] if k in D, else d.  d defaults to None.

get_celltype(celltype)

Return the subset of the instant with only a given element type.

Parameters:

celltype (str) – type of cells in [‘tet’, ‘pyr’, ‘hex’, ‘pri’, ‘tri’, ‘qua’]

Returns:

a copy of the instant with only element of the given type

get_location(location)

Return a copy of the Instant containing only the variables located in the original Instant at the specified location.

Variables (numpy arrays) are NOT deep copied. They are references to the original variables.

Parameters:

location (string in LOCATIONS) – location to extract

Returns:

the Instant with only specified location variables

Return type:

Instant or None

is_structured()

Tell whether the instant is structured or not.

Returns:

the boolean telling if the Instant is structured or not.

Return type:

bool

is_unstructured()

Tells whether the instant is unstructured or not.

Returns:

the boolean telling if the Instant is unstructured or not.

Return type:

bool

keys(location=None, with_shared=True)

Get the list of all variable names.

Force the return type to a list and not KeysView nor dict_keys.

Parameters:

• location (string in LOCATIONS) – if different from None, lists only the variables at the location specified

• with_shared (bool) – if True, it will include the variables contained in the shared Instant

Returns:

the Instant variables

Return type:

list(str) when location is set list(tuple(str, str)) when location is None

mesh_orientation(coordinate_names)

Give the orientation of a 3D structured mesh.

A 3D structured mesh has orientation 1 if at each node, (i, j, k) directions form a right-handed oriented basis. Otherwise, it has a -1 orientation.

The coordinates must be at node.

Parameters:

coordinate_names (list(str)) – the name of variables defining the coordinates

Returns:

1 if right-handed oriented, -1 if left-handed oriented, 0 if undefined

Return type:

int

node_to_cell(variables=None, with_shared=True)

Compute variables at cell centers from values given at nodes.

The parent object is not involved in the process, i.e. the variables contained in a potential associated shared instant are omitted.

Parameters:

• variables (list(str) or None) – list of variables to compute at cell. If None, operate on all variables contained in the object. If a given variable does not exist, it is silently omitted.

• with_shared (bool) – tell if shared variables should be considered. By default, shared variables will be processed.

rel_to_abs(coordinates=['x', 'y', 'z'], conservative_vars=['ro', 'rovx', 'rovy', 'rovz', 'roE'], omega='in_attr', angle='in_attr')

Transform conservative variables in the instant from relative frame to absolute frame.

Parameters:

• coordinates (list(str)) – List of coordinate names.

• conservative_vars (list(str)) – List of conservative variables names in the following order: density, momentum along the x-axis; momentum along the y-axis, momentum along the z-axis and total energy per unit of volume

• omega (float) – Angular speed of the current base. If in_attr use the omega stored in the attrs, necessary if different angular speeds in the base (for example one angular speed per superblock)

• angle (float) – Angular deviation of the current base. If in_attr use the angle stored in the attrs, necessary if different angular deviations in the base (for example one angular deviation per superblock and per instant)

Note

may be moved elsewhere in future releases

Warning

the angular speed must be perpendicular to the x-axis

rename_variables(list_vars, list_newvars, location=None)

Rename variables in the instant.

Parameters:

• list_vars (list(str)) – list of variables to rename

• list_newvars (list(str)) – list of new variable names

• location (str in LOCATIONS) – if different from None, change only the variables at the location specified

Replacement is performed element-wise.

serialized(data=True)

Build a pickable representation of the instant.

set_computer_model(modeling, species_database=None, addons=None)

Setter of the computer.

Parameters:

• modeling (str) – The name of a set of equations. This modeling contains equations (python functions). They can be found in the directory named as the modeling in the directory named formula. ex: the modeling directory internal must be in the directory formula.

• species_database (str) – The filename that contains the information about chemical species in some specific modelings.

• addons (list(str)) – List of additional files (without the python extension) that are located in the directory <modeling_name/formula/addons>.

set_formula(formula)

Setter of the formula.

Parameters:

formula (str) – The name of the new formula.

property attrs

Get the attributes of the Instant.

Return type:

antares.core.AttrsManagement.AttrsManagement

property computer

Get the computer.

property connectivity

Get the connectivities for unstructured grid.

See the section Connectivity for more information.

Returns:

the connectivities for unstructured grid

Return type:

antares.core.CustomDict.CustomDict

property shape

Get the shape of the Instant.

The shape is considered to be the shape of numpy arrays of the node variables contained in the Instant.

Returns:

the shape

Return type:

tuple(int)

---

Connectivity

The connectivity object is an Instant attribute of type CustomDict. It is used to store the connectivity arrays of unstructured grids. An unstructured grid is a collection of points that form geometrical elements (2D or 3D). A mesh element can be described in many ways with its vertices, edges, or faces.

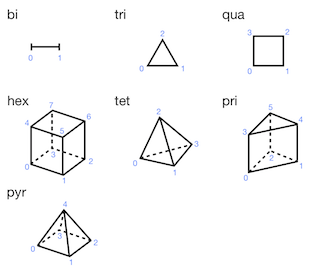
In a vertex-based description, a mesh element is defined with vertices. Antares handle standard (or canonical) linear mesh elements: segment, triangle, quadrilateral, tetrahedron, hexahedron, prism, and pyramid. High-order (quadratic, cubic) mesh elements are not considered. The number of vertices per element (or nodes per cell) for each element type is given by:

Constants.NODES_PER_CELL = {'bi': 2, 'hex': 8, 'pri': 6, 'pyr': 5, 'qua': 4, 'tet': 4, 'tri': 3}

The grid connectivity of each element type is stored in the connectivity attribute:

Instant.connectivity['tri'] = tri_table
Instant.connectivity['qua'] = qua_table

The connectivity table is a two-dimensional numpy array of shape (number of cells of this element type, number of nodes per cell for this element type). The order in which the nodes of a cell are listed is important, and is described in the following picture for the various cell types.

In a face-based description, a mesh element is defined with faces, and the faces are defined with vertices. This enables to tackle with polygons (‘pgon’) and polyhedras (‘phed’).

The grid connectivity of polygons and polyhedras is stored in the connectivity attribute:

poly_conn = PolygonCells()
instant.connectivity['pgon'] = poly_conn

polyhedra = PolyhedronBCells()
instant.connectivity['phed'] = polyhedra

This time, the connectivity is an object of type PolygonCells or PolyhedronBCells.

PolygonCells

Class to store and manipulate polygonal cells.

The polygonal cells are represented as two 1D arrays. The first one stores multiple sorted lists of vertex ids that form each polygon. Care must be taken on the order of the vertices since it determines the orientation of the polygon in the space (see Cells2D documentation). The second one stores the starting index (called “offset”) of each list to enable constant-time random access in the data-structure.

class antares.api.connectivity.PolygonCells.PolygonCells

add_vertices_of_cell(vertex_ids)

Add one cell specified by its sorted vertices.

Parameters:

vertex_ids (list or np.array) – list of ids of vertices representing the cell.

get_number_of_cells()

Give the total number of cells stored in the data-structure.

Returns:

the total number of cells stored in the data-structure.

Return type:

int

get_number_of_vertices()

Alternative len(set(self._c2v)) is slower.

get_vertices_of_cell(cell_idx)

Provide vertex ids of one cell.

Parameters:

cell_idx (int) – the cell from which extract the vertices.

Returns:

the vertex ids as a 1D array.

Return type:

indexable

get_vertices_of_cells(with_offsets=False)

Provide vertex ids of all cells.

The vertex ids are given as a 1D array. If with_offsets flag is set, a list of offsets allowing to do random access on cell array is returned.

Parameters:

with_offsets (bool) – returns list of offsets to identify each cell’s list of faces.

Returns:

an array of vertex ids or a tuple (array of face ids, offsets) if with_offsets flag is set.

Return type:

indexable or tuple

set_vertices_of_cells(c2v, c2v_offsets)

Reset cells to vertices connectivity.

Parameters:

• c2v (np.array) – concatenation of the list of vertices of each cell stored as a 1D array).

• c2v_offsets – list of starting indices of each cell plus the number of data in c2v (stored as a 1D array).

PolyhedronBCells

Class to store and manipulate polyhedral cells with representation (B).

Representation (B) stores the oriented faces forming each polyhedral cell and the vertices forming each polygonal face.

The lists of oriented faces of cells are represented as two 1D arrays. The first one stores multiple sorted lists of face ids that form each cell using the convention for face indices (see Cells3D documentation). Care must be taken on the orientation of faces (see Cells3D documentation). The second one stores the starting index (called “offset”) of each list to enable constant-time random access in the data-structure.

The polygonal faces are represented as two 1D arrays. The first one stores multiple sorted lists of vertex ids that form each polygon. Care must be taken on the order of the vertices since it determines the orientation of the polygon in the space (see Cells3D documentation). The second one stores the starting index (called “offset”) of each list to enable constant-time random access in the data-structure.

class antares.api.connectivity.PolyhedronBCells.PolyhedronBCells

add_faces_of_cell(face_ids)

Add one cell specified by its faces.

Parameters:

face_ids (list or np.array) – list of ids of faces representing the cell.

add_vertices_of_face(vertex_ids)

Add one face specified by its sorted vertices.

Parameters:

vertex_ids (list or np.array) – list of ids of vertices representing the face.

get_faces_of_cell(cell_idx)

Provide face ids of one cell.

Parameters:

cell_idx (int.) – the cell from which extract the faces.

Returns:

the face ids as a 1D array.

Return type:

indexable

get_faces_of_cells(with_offsets=False)

Provide face ids of all cells.

The face ids are given as a 1D array. If with_offsets flag is set, a list of offsets allowing to do random access on cell array is returned.

Parameters:

with_offsets (bool) – returns list of offsets to identify each cell’s list of faces.

Returns:

an array of vertex ids or a tuple (array of face ids, offsets) if with_offsets flag is set.

Return type:

indexable or tuple

get_number_of_cells()

Give the total number of cells stored in the data-structure.

Returns:

the total number of cells stored in the data-structure.

Return type:

int

get_number_of_faces()

Give the total number of faces stored in the data-structure.

One face is counted for two faces having only a different orientation.

Returns:

the total number of faces stored in the data-structure.

Return type:

int

get_number_of_vertices()

Alternative len(set(self._f2v)) is slower.

get_vertices_of_cell(cell_idx)

Provide vertex ids of one cell.

Parameters:

cell_idx (int.) – the cell from which extract the vertices.

Returns:

the vertex ids as a 1D array.

Return type:

indexable

get_vertices_of_cells(with_offsets=False)

Provide vertex ids of all cells.

The vertex ids are given as a 1D array. If with_offsets flag is set, a list of offsets allowing to do random access on cell array is returned.

Parameters:

with_offsets (bool) – returns list of offsets to identify each cell’s list of faces.

Returns:

an array of vertex ids or a tuple (array of face ids, offsets) if with_offsets flag is set.

Return type:

indexable or tuple

get_vertices_of_face(face_idx)

Provide vertex ids of one face.

Parameters:

face_idx (int) – the face from which extract the vertices. If goes from 1 to N_faces or from -1 to N_faces.

Returns:

the vertex ids as a 1D array.

Return type:

indexable

get_vertices_of_faces(with_offsets=False)

Provide vertex ids of all faces.

The vertex ids are given as a 1D array. Only one orientation of each face is stored in this array. If with_offsets flag is set, a list of offsets allowing to do random access on face array is returned.

Parameters:

with_offsets (bool) – returns list of offsets to identify each face’s list of vertices.

Returns:

an array of vertex ids or a tuple (array of face ids, offsets) if with_offsets flag is set.

Return type:

indexable or tuple

set_faces_of_cells(c2f, c2f_offsets)

Reset cells to faces connectivity.

Parameters:

• c2f (np.array) – concatenation of the list of faces of each cell stored as a 1D array).

• c2f_offsets (np.array) – list of starting indices of each cell plus the number of data in c2f (stored as a 1D array).

set_vertices_of_faces(f2v, f2v_offsets)

Reset faces to vertices connectivity.

Parameters:

• f2v (np.array) – concatenation of the list of vertices of each face stored as a 1D array).

• f2v_offsets (np.array) – list of starting indices of each face plus the number of data in f2v (stored as a 1D array).